Hello World 처럼: 카이제곱 검정 제대로 이해하기

카이제곱 검정 제대로 이해하기

1. 개념 이해

비교란 무엇인가?

비교의 대상은 두 개이고 두 비교 대상의 차이를 살펴 보는 것이다.

여기서는 관찰값과 기댓값의 차이를 사용한다.
- 관찰값: 관찰을 통해 얻는 값
- 기댓값: 관찰값에 대한 기댓값으로서 어떤 가정을 바탕으로 함.
두 비교 대상에 대하여 비교할 수 있는 지점은 한 개일 수도 있고 여러 개일 수도 있다.

비교의 목적은 무엇인가?

관찰값과 관찰값을 비교 대상으로 삼을 수는 없는가?
- 비교할 수 있다. 그런데 어떻게 비교할 것인가?
  - 기댓값을 찾고 관찰값들이 기댓값을 중심으로 어떤 분포를 따르는지 이해하는 것이 필요하다.
    - 왜 그런가?
      - 분포를 가정하지 않으면 흔히 일어나는 차이인지 아니면 드물게 일어나는 차이인지 객관적으로 표현하기가 어렵다.
기댓값을 찾으려면 왜 그런 기대를 하게 되었는지와 관련하여 어떤 가정을 세워야 한다.
- 그 가정 위에서 기댓값을 구하고 차이를 계산했더니 흔히 일어나는 차이에 해당하면 그 가정은 유효하다고 간주하고 드물게 일어나는 차이에 해당하면 그 가정은 유효하지 않다고 간주한다.
- 결국 관찰값과 기댓값의 차이를 통해 가정이 유효한지 아닌지 판단하는 것이므로 비교의 목적은 어떤 가정을 채택할 것인지 버릴 것인지를 판단하기 위함이라고 말할 수 있다.

2. 차이의 정도와 의미

차이의 정도를 수치로 나타낼 수 있는가?

비교 대상 간의 총체적인 차이는 무엇으로 정의할 것인가?

개별 데이터 지점에서의 차이 값의 제곱의 합이라고 정의하자. 절대값의 합이 아니라 제곱의 합으로 정의한 이유는 수학적으로 다루기가 훨씬 쉽기 때문일 것이다.
아래의 수식은 피어슨 카이제곱 통계량이고 이것으로 총체적인 차이를 계산한다. $O_i$ 는 $i$ 번째 데이터 지점에서의 관찰값, $E_i$ 는 $i$ 번째 데이터 지점에서의 기댓값을 나타낸다.

$\chi^2 = \sum_{i=1}^{m} \frac {(O_i-E_i)^2}{E_i} \tag{1}$

특정 값의 총체적인 차이가 발생할 가능성은?

차이의 정도에 대한 가정
- 개별 데이터 지점에서 관찰값과 기댓값의 차이의 정도는 확률변수이고 정규분포를 따른다.
  - 오차에 대한 가정을 주로 이렇게 한다는 점을 참고하자.
  - 편차 제곱을 기댓값으로 나눔으로써 표준화를 시도한다.
- 모든 데이터 지점에서 기댓값은 5 이상이어야 한다.
  - 대표본 가정
그렇다면 총체적인 차이가 특정 값 이상일 가능성은?
- 총체적인 차이 값은 확률변수이고 자유도를 파라미터로 하는 카이제곱 분포를 따른다.
  - 좀 더 정확하게 표현하자면 이런 경우의 분포를 카이제곱 분포라고 정의한 것이다.
- 카이제곱 분포표에서 자유도와 유의수준에 해당하는 카이제곱 값을 찾을 수 있다.
  - 총체적인 차이가 카이제곱 분포표에서 찾은 카이제곱 값보다 작으면 흔히 일어날 수 있는 차이로 간주하고 그렇지 않으면 쉽게 일어나기 어려운 차이로 간주한다.

차이의 정도가 유의미한가?

유의수준 $\alpha$ 를 설정한다. 여기서는 $\alpha = 0.05$ 로 하자.
자유도가 얼마인지 파악한다.
개별 데이터 지점에 대하여 기댓값을 파악하거나 계산한다.
피어슨 카이제곱 통계량을 계산한다.
카이제곱 분포표에서 자유도와 유의수준에 해당하는 카이제곱 값을 찾는다.
계산한 카이제곱 값이 분포표에서 찾은 카이제곱 값보다
- 작으면 차이가 유의미하지 않다고 보고 대립가설을 기각한다.
- 크면 차이가 유의미하다고 간주하고 대립가설을 채택한다.

차이가 유의미하다는 것은 무슨 뜻인가?

검정 목적별로 해석을 달리한다.

적합도 검정 (Goodness-of-fit Test)
- 주머니속 사탕 색깔의 구성 비율이 특정 비율을 따르는지? ⇒ 구성 비율에 대한 추측이 사실이 아닐 가능성이 높다.
동질성 검정 (Test of Homogeneity)
- 성별에 따른 메뉴 선호도가 유사한지? ⇒ 성별에 따른 메뉴 선호도가 유사하지 않을 가능성이 높다.
독립성 검정 (Test of Independence)
- 성별과 메뉴 선호도가 서로 관련이 없는지? ⇒ 성별과 메뉴 선호도가 서로 관련이 있을 가능성이 높다.

다음 두 가지 설명이 동질성 검정과 독립성 검정의 차이를 이해하는데 도움이 될 것이다.

독립성 검정의 결과
- 서로 관련이 없다.
  - 동질성 검정 필요 없음
- 서로 관련이 있다.
  - 동질성 검정의 결과
    - 유사하다.
    - 유사하지 않다.
      - 서로 관련은 있으나 유사하지는 않은 경우
        
        예를 들자면 남자가 좋아하는 메뉴는 여자가 싫어하고 남자가 싫어하는 메뉴는 여자가 좋아함
동질성 검정의 결과
- 유사하다.
  - 독립성 검정 필요 없음
- 유사하지 않다.
  - 독립성 검정의 결과
    - 서로 관련이 없다.
    - 서로 관련이 있다.
      - 유사하지는 않으나 서로 관련은 있는 경우
        
        예를 들자면 남자가 좋아하는 메뉴는 여자가 싫어하고 남자가 싫어하는 메뉴는 여자가 좋아함

카이제곱 검정 예를 좀 더 구체적으로 살펴 본다면?

적합도 검정
- 관찰값의 분포를 통해 모집단의 분포를 확인하는 검정
  - 예시: 주머니 속 사탕을 복원추출하여 파악한 색깔 구성 비율을 토대로 주머니 속 사탕 색깔이 골고루 섞여 있다고 볼 수 있는지?
    - 첫 번째 행은 관찰도수, 두 번째 행은 기대도수
    - 관찰도수와 기대도수의 차이를 사용하여 $\chi^2$ 구하기
동질성 검정
- 각기 다른 모집단으로부터 표본을 추출하여 특성 값에 따라 분류하고 두 모집단의 특성 값 비율이 유사한지 검정
  - 예시: 성별에 따른 메뉴 선호도가 유사한지?
    - 행은 집단, 열은 특성 값
    - 행의 주변도수 크기 고정
    - 열의 주변도수(marginal frequency)를 구하고 이들의 분포를 활용하여 각 행의 특성 값들에 대하여 기대도수 구하기
    - 관찰도수와 기대도수의 차이를 사용하여 $\chi^2$ 구하기
독립성 검정
- 두 종류 이상의 범주형 변수를 사용하여 자료를 분류하였을 때 변수들이 서로 독립적인지 검정
  - 예시: 성별과 메뉴 선호도가 서로 관련이 없는지?
    - 표본 크기 고정
    - 두 변수가 서로 독립적이다라는 전제로 기댓값 구하기
    - 관찰도수와 기대도수의 차이를 사용하여 $\chi^2$ 구하기

카이제곱 검정의 세 종류는 서로 다른 목적을 가지고 있지만 공통점은 다음과 같다.

관찰값과 기댓값의 차이를 계산한다. 관찰값과 관찰값의 차이를 계산하는 것이 아님에 주목하자.

더 많은 예시

적합도 검정
- 멘델의 유전법칙에 의하면 4종류의 식물이 9:3:3:1의 비율로 나오게 되어 있다고 한다. 240그루의 식물을 관찰하였더니 120:40:55:25로 나타났다. 유의수준 5%로 적합도 검정을 하시오
- 어느 공정의 부적합품률은 15%로 알려져있다. 시료를 80개 추출하여 검사한 결과 불량이 16개이다. 유의수준 5%로 적합도 검정을 하시오.
- 두 정당에 대한 지지율이 한 달 전에는 54:46이었다.
동질성 검정
- 남,녀 각각 500명을 임의로 추출하였고, 성별에 따른 선호도가 관련성이 있는지, 유의수준 0.05에서 검정하시오.
- 기존약과 신약의 효과 비교
- 성별에 따른 흡연 여부의 분포
독립성 검정
- 영화 장르와 간식류 구매는 서로 연관이 있는지 검정하시오.
- 보호구 착용과 부상 정도
- 성별과 흡연 여부의 관련성

3. 카이제곱 분포와 검정

카이제곱 분포

양의 정수 $k$ 에 대하여 $k$ 개의 독립적이고 표준정규분포를 따르는 확률변수 $X_1$ , …, $X_k$ 를 정의하면 자유도 $k$ 의 카이제곱 분포는 확률변수

$Q = \sum_{i=1}^{k} X_i^2 \tag{2}$

가 따르는 분포입니다.

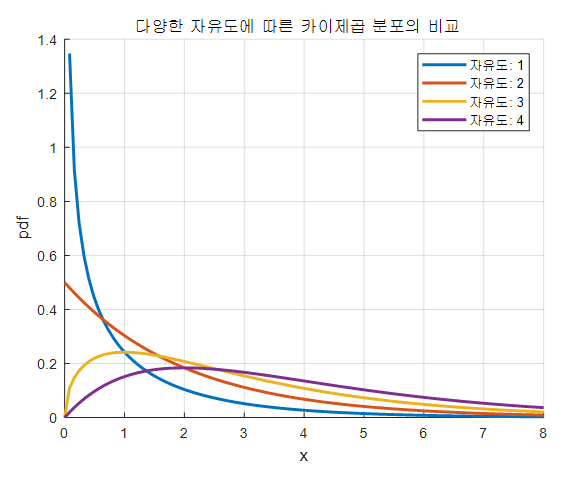
이미지 출처: 카이제곱 분포와 검정, 공돌이의 수학정리노트

피어슨 카이제곱 통계량

$\chi^2 = \sum_{i=1}^{m} \frac {(O_i-E_i)^2}{E_i} \tag{3}$

기댓값을 파악한다.
관찰값과 기댓값의 차이를 구하여 제곱하고 기댓값으로 나눔으로써 정규화를 한다.
각각의 관찰 속성에 대하여 위와 같이 구한 값을 더한다.

모든 관찰값이 5 이상이면 카이제곱 분포 식 (1)에 근사한다고 증명되어 있다.

관찰값이 5보다 작은 경우라면 카이제곱이 아니라 피셔의 정확 검증 시도

카이제곱 검정

예를 들어 자유도 $k$ 인 카이제곱 분포에 대해 아래와 같이 검정을 수행한다.

유의수준 $\alpha$ 를 정한다.
- 예: $\alpha = 0.05$
자유도 $k$ 인 확률변수의 관찰값들에 대하여 카이제곱 값 $Q$ 를 구한다.
- 예: $k = 2$ => $Q = 6.1$
카이제곱 분포표에서 자유도 $k$ 인 경우 유의수준 $\alpha$ 에 해당하는 카이제곱 값 $\chi^2$ 을 찾는다.
- 예: $k = 2, \alpha = 0.05$ => $\chi^2 = 5.99$
계산한 카이제곱 값이 카이제곱 분포표에서 찾은 값보다 크면 귀무가설을 기각하고 대립가설을 채택한다.
- 예: $Q > \chi^2$ => 차이가 유의하므로 귀무가설 기각, 대립가설 채택

참고 자료

13. 비모수통계
카이제곱 분포와 검정, 2021.12.13, 공돌이의 수학정리노트
[이론] 카이제곱 검정(Chi-Squared Test)이란?, 2021.04.10, 꿈꾸는 직장인
카이제곱 분포 이해하기, 2022.04.19, 의미를 이해하는 통계학과 데이터 분석
독립성검정과 동질성검정의 차이(feat.카이제곱 검정), 2021.3.20, 통계의 본질
카이제곱 분포표 보는 법, 2019.11.04, 나부랭이의 수학블로그
Engineering Tables/Chi-Squared Distribution, Wikibooks

Written with StackEdit.

Hello World 처럼

페이지

2024년 7월 27일 토요일