Hello World 처럼: 가설 검정 제대로 이해하기

가설 검정 제대로 이해하기

(주의: 공부하면서 작성하는 문서라서 오류가 있을 수 있습니다.)

1. 문제 정의

1.1. 사례

기존 가설: 20 대 한국인 남성의 100 미터 달리기 평균 속도는 17 초
새로운 실험 결과: 무작위로 추출한 20 대 한국인 남성 500 명의 100 미터 달리기 평균 속도는 16 초

위 사례에서 새로운 실험 결과가 우연히 일어났다고 보는 것이 적절할까요 아니면 가설이 유효하지 않은걸까요? 정답이 존재하지 않는 이런 종류의 문제를 다루기 위해서는 차이가 얼마나 의미있는지 표현하는 객관적인 방법이 있어야 하지 않을까요?

1.2. 문제

기존 가설과 새로운 실험의 결과가 양립하는 정도를 체계적인 과정을 통해 숫자로 표현하는 방법은 무엇인가?

2. 용어 정리

2.1. 출처: 위키백과, WIKIPEDIA

통계적 추론
- 추론 통계 또는 추론 통계학(inferential statistics)으로 불린다.
- 기술 통계학(descriptive statistics)과 구별되는 개념
- 도수 확률(frequency probability)과 사전 확률(prior probability)을 기반으로 하는 베이즈 추론의 두 학파가 있다.
- 추정(estimation)과 가설 검정(hypothesis test)으로 나눌 수 있다.
가설 검정
- 통계적 가설 검정(statistical hypothesis test)
- 모집단 실제의 값이 얼마가 된다는 주장과 관련해, 표본의 정보를 사용해서 가설의 합당성 여부를 판정하는 과정
- 가설 검정 또는 가설검증(hypothesis test)이라고 부르는 경우도 많다.
통계적 가설
- 하나의 특정 주장을 모수를 이용해 나타낸 형태를 지칭
- 귀무가설(Null hypothesis, $H_0$ , 영가설)과 이와 반대에 있는 대립가설(Alternative hypothesis, $H_1$ )로 나타낸다.
모수
- 매개변수(媒介變數), 파라미터(parameter), 모수(母數)는 수학과 통계학에서 어떠한 시스템이나 함수의 특정한 성질을 나타내는 변수
- 함수의 수치를 정해진 변역에서 구하거나 시스템의 반응을 결정할 때는 독립변수는 변하지만 매개변수는 일정
가설 검정 5단계 절차
1. 유의수준의 결정, 귀무가설( $H_0$ )과 대립가설( $H_1$ ) 설정
2. 표집(sampling) 및 검정통계량의 설정
3. 기각역의 설정
4. 검정통계량 계산 및 영가설 확인
5. 통계적인 의사결정
유의 확률
- 유의 확률(有意確率, 영어: significance probability, asymptotic significance) 또는 p-값(영어: p-value, probability value)은 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률이다.
- p-값(p-value)은 귀무 가설(null hypothesis)이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 ‘같거나 더 극단적인’ 통계치가 관측될 확률이다. 여기서 말하는 확률은 ‘빈도주의’ (frequentist) 확률이다.
- p-값(p-value)는 관찰된 데이터가 귀무가설과 양립하는 정도를 0에서 1 사이의 수치로 표현한 것이다. p-value가 작을수록 그 정도가 약하다고 보며, 특정 값 (대개 0.05나 0.01 등) 보다 작을 경우 귀무가설을 기각하는 것이 관례
귀무가설과 대립가설 설정
- 양측 검정(two-sided test, two-tailed test)
  - 기각 영역(rejection region)이 양쪽에 있는 것이고, 그러므로 유의수준도 양 극단으로 갈라져 한쪽의 면적이 절반이 된다.
- 단측 검정(one-sided test)
  - 좌측 검정(lower tailed test)
  - 우측 검정(upper tailed test)
표본 분포(sampling distribution)
- 표본 분포(sampling distribution 또는 finite-sample distribution) 또는 표집분포는 크기 n의 확률 표본(random sample)의 확률 변수(random variable)의 분포(distribution)이다.
- 모집단에서 임의로 추출된 표본의 평균을 표본 평균이라고 하며 표본 평균도 그 값이 변하는 확률 변수인데 그 확률 분포를 표본 평균의 분포라고한다.
  - 표준 오차는 이 분포의 표준 편차이다.
- 특히 표집 분포(sampling distribution)는 연구 대상이 되는 모집단에서 다중 복수의 표본들을 추출한 자료들을 통해서 통계적 가설을 검증할 때 필요한 분포이다. 따라서 모집단으로부터의 충분한 여러 표집(sampling)에서 얻게되는 표본들의 표본평균들은 표집분포를 갖게되고 이 표집 분포는 모집단의 분포에 수렴한다.
  - 이러한 중심극한정리(cetral limit theorem)에서 표집 분포의 평균값( $\mu_{\bar X}$ )은 모집단의 평균값( $\mu$ )에 근사하게 된다. ⇐ 가설 검정의 기반 !!!
검정 통계량(test statistic)
- 통계적 가설 검정(statistical hypothesis testing)에 사용할 목적으로 표본으로부터 유도한 값
- 검정 통계량의 중요한 성질은 귀무가설 하에서 검정 통계량의 표집 분포를 정확하게 또는 근사적으로 계산할 수 있어야 한다는 것이고 그럴 수 있어야 p-value를 계산하는 것이 가능해진다.
- 검정 통계량은 기술 통계량과 일부 동일한 성질을 공유하고 있으며 많은 통계량들이 검정 통계량으로 그리고 기술 통계량으로도 쓰일 수 있다.
- 검정 통계량은 통계적 가설 검정을 위해 특별히 고안된 것인데 반해 기술 통계량은 쉽게 해석될 수 있다.
- 예를 들어 표본의 범위는 중요한 정보를 제공하는 기술 통계량이지만 그것들의 표집 분포를 결정하는 것은 어려우므로 검정 통계량으로 사용하기에는 적절하지 않다.
- 가장 널리 사용되는 검정 통계량과 통계적 가설 검정 모델
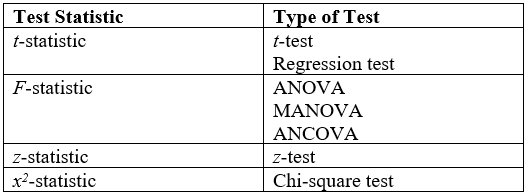
- 널리 사용되는 검정 통계량 두 가지는 t-statistic과 F-statistic
1종 오류와 2종 오류
- 1종 오류 - 귀무가설을 잘못 기각하는 오류
  - 거짓 양성 또는 알파 오류라고도 한다.
- 2종 오류 - 귀무가설을 잘못 채택하는 오류
  - 거짓 음성 또는 베타 오류라고도 한다.
t-검정
- t-검정 (t-test) 또는 스튜던트 t-테스트 (Student’s t-test)는 검정통계량이 귀무가설 하에서 t-분포를 따르는 통계적 가설 검정법이다.
- 예를 들어 t-테스트를 사용하여 두 데이터 세트(집단)의 평균이 서로 유의하게 다른지 여부를 판별할 수 있다.
t값
- t값(t score)은 z값(z score)이 소수(小數)로서 음수와 양수에 걸쳐 분포하는 것을 재설정해줌으로써 자연수와 백분위수로 표현해 보여줄 수 있다는 점에서 데이터의 가독성을 보다 높인 값이다.
카이제곱 검정
- 카이제곱 검정(chi-squared test) 또는 $\chi ^2$ 검정은 카이제곱 분포에 기초한 통계적 방법으로, 관찰된 빈도가 기대되는 빈도와 의미있게 다른지의 여부를 검정하기 위해 사용되는 검정방법이다. 자료가 빈도로 주어졌을 때, 특히 명목척도 자료의 분석에 이용된다.
- 카이제곱 값의 계산: $\chi ^2 = \sum \frac{(관측값 - 기댓값)^2}{기댓값}$
- 동질성 검정과 독립성 검정 두 유형이 있다.
검정력
- 대립가설이 사실일 때, 이를 사실로서 결정할 확률이다.
자유도
통계적 유의성

검정통계량은 표본 크기의 함수이므로 표본 크기가 커질수록 검정통계량의 값은 커져서 실질적으로는 유의성이 없어도 통계적으로는 유의한 것으로 판정될 수 있다. 이때의 오류는 1종오류가 된다. 즉, 통계적 유의성은 오류가능성을 동반한다.

2.2. 부연 설명

유의 수준
- 귀무가설 하에서의 검정통계량과 실험 표본의 검정통계량의 차이가 유의미하다고 말할 수 있는 수준
- 유의 수준을 0.05로 정한다는 말의 의미:
  - 귀무가설이 유효하다는 전제 하에서는 실험 표본의 검정통계량이 발생할 확률이 5% 미만이다.
- 귀무가설이 유효하다는 전제 하에서는 쉽게 발생할 수 없을 것이라고 생각했던 사건이 관찰되었다면 우연히 일어난 것이거나 귀무가설 자체가 유효하지 않아서일 가능성이 있다. 이럴 때 차이가 의미있다고 판단하기 위해 사용할 기준, 즉 유의 수준을 미리 정해 놓았다면 그것과 비교해서 귀무가설을 선택하거나 기각하면 된다.
  - 이러한 비교가 가능하려면 통계 모델이 있어야 하고 그에 따른 검정통계량을 계산할 수 있어야 한다. 그리고 계산된 검정통계량의 값으로부터 유의 확률(p-value)을 알 수 있는 참조 테이블이 필요하다.

3. 통계적 가설 검정 예시

예시를 통해서 구체적으로 설명해 보겠습니다.

유의수준의 결정, 귀무가설( $H_0$ )과 대립가설( $H_1$ ) 설정
- 유의 수준: $p > .05$ (공식적인 표기는 소수점 앞의 '0’을 생략)
- 귀무가설: 20 대 한국인 남성의 100 미터 달리기 평균 속도는 17 초
- 대립가설: 20 대 한국인 남성의 100 미터 달리기 평균 속도는 17 초가 아님
표집(sampling) 및 검정통계량의 설정
- 크기가 $n$ 인 표본 집단 선정
- 검정통계량: 표본 평균
- 귀무가설 하에서 크기가 $n$ 인 표본 집단의 표본 평균의 표집 분포를 계산

$\bar X \sim N(\mu, \frac{\sigma^2}{n})$

기각역의 설정
- 양측 검정
검정통계량 계산 및 영가설 확인
- 관찰 표본의 표본 평균으로 앞에서 계산한 표집 분포 상의 p-value를 계산
  - 확률 분포 $\bar X \sim N(\mu, \frac{\sigma^2}{n})$ 상에서 관찰 표본의 표본 평균이 좌측 꼬리에 있을 경우 표본 평균 이하의 값이 나올 확률이 p-value, 우측 꼬리에 있을 경우 표본 평균 이상의 값이 나올 확률이 p-value
통계적인 의사결정
- $value > \frac{0.05}{2}$ 이면 귀무가설 채택, $value <= \frac{0.05}{2}$ 이면 귀무가설 기각

4. 더 읽어 볼 만한 자료

검정 통계량, 정보통신기술용어해설
표집분포의 이해, 2020.01.08, DB의 DB
가설검정 방법과 유의수준, p 값(p value) 개념 정리, 처음부터 배우는 데이터과학
- 예시: 혈압 개선 약품의 효능 검정
T 검정과 Z 검정이란? 두 집단 차이를 통계적으로 검증하기, 2022.03.03, 처음부터 배우는 데이터과학
- 예시: 쇼핑몰의 지역별 객단가 분석
- z검정과 t검정의 차이에 대한 간략한 설명
카이제곱 분석 이해하기, 2023.09.23, 게으름의 흔적
- 예시: 대학에서 전공(과학, 예술)과 학습 스타일(집단 학습, 개별 학습)의 관계에 대해 조사
데이터 분석 초보자를 위한 T-test & Chi-squared test, 2020.09.18, Gayeon Kim

각 가설 검정 방법은 각자가 검정할 수 있는 가설의 형태가 미리 정해져 있으며, 우리는 이를 임의로 바꿀 수 없다.
- 귀무가설 예시
  - t 검정
    - 예시-1. Adelie 펭귄의 평균 몸무게는 8kg일 것이다.
    - 예시-2. Adelie 펭귄의 평균 몸무게는 3.72kg일 것이다.
    - 예시-3. Adelie 펭귄의 평균 부리 깊이와 Gentoo 펭귄의 평균 부리 깊이는 같다.
    - 예시-4. Adelie 펭귄의 평균 부리 깊이와 Chinstrap 펭귄의 평균 부리 깊이는 같다.
  - 카이제곱 검정
    - 예시-5. 펭귄의 성비는 1:1일 것이다. (적합성 검정)
    - 예시-6. 펭귄의 몸무게와 플리퍼 길이는 연관이 없다. (독립성 검정)
파이썬 카이제곱 검정 예, 2023.06.27, 사막의 수도자
- 예시-1. 가족의 크기에 따라 구매하는 차의 크기가 다른지 검정 (독립성 검정)
- 예시-2. 요일별 커피 판매량이 다른지 검정 (적합성 검정)
[통계] t검정(T-test), 2023.05.24, nbac406
- 예시-1. 게임A와 게임B의 평균 플레이 시간은 같은지 검정
- 예시-2. 강남과 강북의 휘발유 평균 차이는 있는지 검정
[이론] 카이제곱(Chi-Squared Test) 검정이란?, 2021.04.10, 꿈꾸는 직장인
- 카이제곱 검정 유형: 적합도 검정, 동질성 검정, 독립성 검정
- 예시. 연령과 선호 SNS가 서로 독립인지 검정 (계산 과정을 구체적으로 보여 줌)

Written with StackEdit.

Hello World 처럼

페이지

2024년 5월 7일 화요일