차등 정보보호 - 예시

다섯 명의 환자 질병 유무 데이터에 불확실성을 추가하여 공개하고 이로부터 원래의 질병 보유 환자 비율이 어떤 값일지 추정하는 과정을 보여 줍니다.

불확실성 추가 방식 정하기

전체 영역 중에서 밝은 부분의 면적이 차지하는 비율이 90%인 스피너를 사용하여 원본 데이터에 불확실성을 추가합니다.

• $p_{light} = 0.9$

시행 결과로 바늘이 밝은 부분에서 멈추면 질병 유무를 그대로 유지하고 어두운 부분에서 멈추면 질병 유무를 뒤집어서 기록합니다.

원본 데이터 준비하기

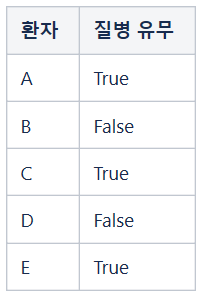
위의 데이터는 원본이기 때문에 환자 D의 False가 진짜 False일 가능성은 100%입니다.

불확실성 추가하기

환자별로 스피너를 시행하고 그 결과에 따라 질병 유무를 그대로 유지하거나 반대로 바꿉니다.

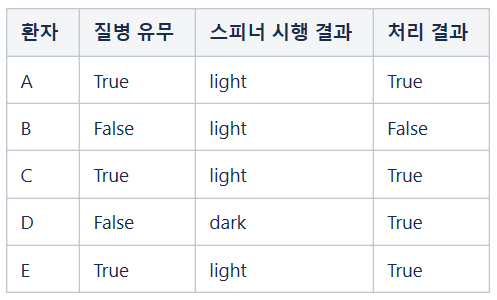
데이터 공개하기

스피너를 시행하여 처리한 결과 데이터를 공개합니다.

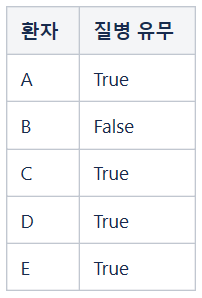
불확실성의 추가로 인해 환자 D의 True가 진짜 True일 가능성은 100%가 아니고 90%가 됩니다. 이것은 다른 환자들의 질병 유무에 대해서도 마찬가지입니다.

질병 보유 비율 추정

공개된 데이터로부터 원본 데이터의 질병 보유 비율을 추정합니다.

통계 자료

원본 데이터에서 질병 유무가 True인 환자의 비율:

• $n_{original} = 0.6$

공개 데이터에서 질병 유무가 True인 환자의 비율:

• $n_{public} = 0.8$

수식 유도

공개 데이터로부터 추정하는 원본 데이터에서 질병 유무가 True인 환자의 비율:

• $n_{estimated} = ?$

공개 데이터에서 질병 유무가 True인 환자는 진짜 True인 환자가 True로 대답했거나 진짜 False인 환자가 True로 대답한 경우에 해당합니다. 따라서 다음의 관계가 성립합니다.

• $n_{public} = n_{estimated} \times p_{light} + (1 - n_{estimated}) \times (1 - p_{light})$

위의 관계를 사용하여 질병 유무가 진짜 True인 환자의 비율을 추정할 수 있습니다.

• $n_{estimated} = \frac {n_{public} - (1 - p_{light})}{2 \times p_{light} - 1} = \frac {0.8 - (1 - 0.9)}{2 \times 0.9 - 1} = \frac {0.7}{0.8} = 0.875$

오차율

진짜 True 환자 비율과 추정 True 환자 비율의 차이:

• ${error} = n_{estimated} - n_{original} = 0.875 - 0.6 = 0.275$

참고 자료

• Differential privacy, an easy case — 2019–01–03, Mark Hansen

Written with StackEdit.